State space search: the basics
A while back, briefly discussing Steve McConnell's Code Complete, I wrote, "On the other hand, McConnell previously presented as a good use of recursion a maze-solving function; maze solving is an application of state-space search, which has a simple, clear, and wildly flexible iterative implementation based on a priority queue." Between that, and the Stanford AI course (which only briefly mentioned most of what I spent a semester learning back in the late '80's), I have been pondering state space search lately. It really is an elegant algorithm. So, I thought I'd spend some spare time writing an elaborate and likely unnecessary post or three about it.
I'll begin with a state. A state is a particular configuration of the system in question. For example, a board position in chess is a state. When you place the pieces on the board, you create an initial state; after some number of moves, the board is in some other state. When the game is over, the board is in a terminal state; if you won, it's in a goal state, but the difference is the topic of some other post. For the moment, I will only be talking about systems where the only terminal states are goals.
A state space is the set of all possible states for a system. For chess, the state space is all possible board positions, and there are a lot of them. Chess has a fairly large state space. The states in a state space are related by the valid actions of the system; given a state those actions produce a collection of the next states reachable by one operation of the system. For chess, the actions are the valid moves of individual chess pieces and, because the initial state is defined by the rules of chess, the state space includes all board positions reachable from that initial state by legal chess moves.
State space search is the technique of searching for a goal state, beginning with an initial state and using the operations available in each state to generate new states. Or, alternatively, beginning with a goal state and searching for a suitable initial state. Or possibly even starting with an initial state and a goal state and searching for a way to connect the two in the state space. Each of those approaches is suitable for some problems, depending on the nature of the problem. The key point is to explore the state space of the problem, searching for a solution.
State space search is one of the most powerful techniques in computer science. If a problem can be framed in a way suitable to state space search (and most can), then the algorithm is guaranteed to find a solution. Theoretically, anyway. If you have a problem and do not have any more direct algorithm, it is the go-to way to solve it. Or, at least it was; there are other techniques that have become popular, usually for very good reasons.
On the other hand, state space search has some serious weaknesses. For one thing, not all problems can be usefully framed in terms of a state space. It requires that the problem be both discrete and deterministic; discrete in such a way that all states are distinct from one another and deterministic so that an action produces exactly one subsequent state from an input state. But that is not the worst part. State space search is the poster child for exponential algorithms. I said it was guaranteed to find a solution, but I carefully didn't say you would be alive to see it. Or, anything would be alive to see it. But there are plenty of problems to which state space search is applicable.
The algorithm
So, with all that buildup, the algorithm is a typical let-down:
def search(queue):
while not empty?(queue):
current_state := remove_element(queue)
if is_goal?(current_state):
return current_state
for next_state in expand(current_state):
if not seen?(next_state):
mark_seen(next_state)
add(queue, next_state)
return nil
The intelligence of the algorithm is actually in the:
- Queue that is used to store states before they are examined and expanded and which determines the nature of the search,
- The rules that determine whether a state is a goal and how the state is expanded into subsequent states, and
- The set used to determine whether a state has been seen before; this and the queue will determine how much memory the algorithm uses.
How does this look in Java?
public T findGoal()
{
while (!queue.isEmpty())
{
statesExamined++;
T current = queue.remove();
if (current.isGoal())
{
return current;
}
for (T newState : current.expand())
{
if (!seen.contains(newState))
{
seen.add(newState);
queue.add(newState);
}
}
}
return null;
}
statesExamined is an accounting addition, just used for entertainment purposes. The rest of the class similarly simple, initializing seen and queue based on constructor arguments. Like I said, nothing up my sleeve....
public class Search<T extends State<T>>
{
private int statesExamined;
private final Queue<T> queue;
private final Set<T> seen;
public Search(Queue<T> queue, Set<T> seen, T initialState)
{
this.queue = queue;
queue.add(initialState);
this.seen = seen;
this.statesExamined = 0;
}
[...findGoal...]
public int statesExamined()
{
return statesExamined;
}
}
The Set seen is used to prevent states from being expanded repeatedly. It records when a state is first seen and subsequently prevents it from being re-added to the queue. Without this, the algorithm could enter an infinite loop if the state space is not acyclic.
The State interface is not much more interesting. The only required methods are to expand the state, producing a list of subsequent states produced by valid actions, and a predicate that is true if the state is a goal.
If the state space search code is so simple, how is the algorithm capable of such power? How about an example?
public interface State
{
public Listexpand();
public boolean isGoal();
}
Missionaries and cannibals: rivercrossing
The problem is, according to Gerhard Wickler,
On one bank of a river are three missionaries and three cannibals. There is one boat available that can hold up to two people and that they would like to use to cross the river. If the cannibals ever outnumber the missionaries on either of the river’s banks, the missionaries will get eaten.
How can the boat be used to safely carry all the missionaries and cannibals across the river?
(I have seen versions where the threat is the missionaries converting the cannibals, rather than the cannibals cannibalizing (ahem) the missionaries. I am a traditionalist, however.)
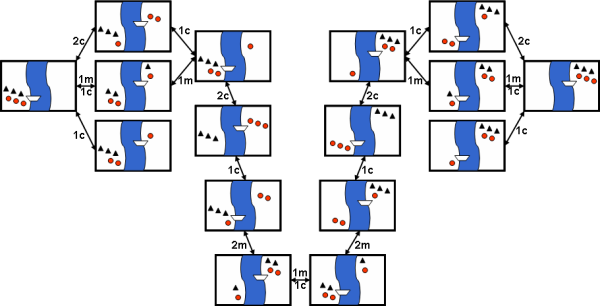
Gerhard Wickler also has an excellent illustration of the complete state space for this problem. The initial state is on the left; the goal state is on the right. With 16 states, the state space is tiny in comparison with the space of other problems, but it gets my point across.
Each state is a configuration of the missionaries and cannibals on each side of the river as well as which shore the boat is on. The process of crossing the river is abstracted away; each state transition involves the boat, with at least one passenger, crossing the river.
Specifically, a state in the puzzle is made up of the participants on this side of the river, the participants on that side of the river, and the location of the boat, this side or that side.
private static enum BoatSide { THIS, THAT };
On either side of the river are some number of missionaries and cannibals. I abstracted out the state of each side of the river as a class. There are a couple of special features of RiverSide, though.
- First, the class includes methods
missionaries,cannibals, andbothwhich returns a newRiverSideinstance with the number of missionaries or cannibals modified. These are used when generating new states while expanding a given state. - Second, the class implements
equalsandhashCode, making instances eligible to be stored in aHashMap.
private static class RiverSide
{
public final int missionaries;
public final int cannibals;
public RiverSide(int missionaries, int cannibals)
{
this.missionaries = missionaries;
this.cannibals = cannibals;
}
public RiverSide missionaries(int n)
{
return new RiverSide(missionaries + n, cannibals);
}
public RiverSide cannibals(int n)
{
return new RiverSide(missionaries, cannibals + n);
}
public RiverSide both(int n)
{
return new RiverSide(missionaries + n, cannibals + n);
}
@Override
public boolean equals(Object o)
{
if (! (o instanceof RiverSide)) return false;
final RiverSide other = (RiverSide) o;
return this.missionaries == other.missionaries
&& this.cannibals == other.cannibals;
}
@Override
public int hashCode()
{
return missionaries ^ cannibals;
}
@Override
public String toString()
{
return String.format("[%d missionaries, %d cannibals]", missionaries, cannibals);
}
}
There are two constructors for the state class: the first, public, one creates the initial state for the problem, with three missionaries, three cannibals, and the boat on this side of the river. The second, private, one creates a new MCState based on a previous one and updated inhabitants of this and that side. The previous state is recorded so that the program can reconstruct the sequences of moves in a solution.
The methods required for State are next. isGoal is implemented by checking how many missionaries and cannibals are on that side of the river. expand is more complex, but breaks down into a number of branches; if the boat is on this side of the river, then expand generates all possible ways for it to get to the other side of the river, carrying one or two missionaries or cannibals; if the boat is on the other side, it does the reverse. Specifically, it collects a list of subsequent states; if at least one missionary is on this side, then a possible next state has the boat and one more missionary on that side. Likewise, if there are two missionaries on this side with the boat, another next state would be two less missionaries on this side and two more and the boat on that. The same logic applies to the cannibals and to a missionary and a cannibal moving to the other side. All of these branches go through queueNewState, which first checks whether the new state is invalid if it presents the opportunity for some cannibals to devour some missionaries. As a result of the branches, each state has five possible next states, although some (or most) of those states are invalid.
MCState also implements hashCode and equals, making instances eligible for HashSet storage.
public class MCState implements State<MCState>
{
[...]
public final BoatSide boatSide;
public final RiverSide thisSide;
public final RiverSide thatSide;
public final MCState previous;
public MCState()
{
boatSide = BoatSide.THIS;
thisSide = new RiverSide(3, 3);
thatSide = new RiverSide(0, 0);
previous = null;
}
private MCState(MCState previous, RiverSide thisSide, RiverSide thatSide)
{
this.boatSide = previous.boatSide == BoatSide.THIS ? BoatSide.THAT : BoatSide.THIS;
this.thisSide = thisSide;
this.thatSide = thatSide;
this.previous = previous;
}
@Override
public boolean isGoal()
{
return thatSide.missionaries == 3 && thatSide.cannibals == 3;
}
@Override
public List<MCState> expand()
{
List<MCState> newStates = new ArrayList<MCState>();
if (boatSide == BoatSide.THIS)
{
if (thisSide.missionaries > 0)
{
final MCState newState =
new MCState(this, thisSide.missionaries(-1), thatSide.missionaries(1));
queueNewState(newStates, newState);
}
if (thisSide.missionaries > 1)
{
final MCState newState =
new MCState(this, thisSide.missionaries(-2), thatSide.missionaries(2));
queueNewState(newStates, newState);
}
if (thisSide.cannibals > 0)
{
final MCState newState =
new MCState(this, thisSide.cannibals(-1), thatSide.cannibals(1));
queueNewState(newStates, newState);
}
if (thisSide.cannibals > 1)
{
final MCState newState =
new MCState(this, thisSide.cannibals(-2), thatSide.cannibals(2));
queueNewState(newStates, newState);
}
if (thisSide.missionaries > 0 && thisSide.cannibals > 0)
{
final MCState newState =
new MCState(this, thisSide.both(-1), thatSide.both(1));
queueNewState(newStates, newState);
}
}
else
{
if (thatSide.missionaries > 0)
{
final MCState newState =
new MCState(this,thisSide.missionaries(1), thatSide.missionaries(-1));
queueNewState(newStates, newState);
}
if (thatSide.missionaries > 1)
{
final MCState newState =
new MCState(this,thisSide.missionaries(2), thatSide.missionaries(-2));
queueNewState(newStates, newState);
}
if (thatSide.cannibals > 0)
{
final MCState newState =
new MCState(this,thisSide.cannibals(1), thatSide.cannibals(-1));
queueNewState(newStates, newState);
}
if (thatSide.cannibals > 1)
{
final MCState newState =
new MCState(this,thisSide.cannibals(2), thatSide.cannibals(-2));
queueNewState(newStates, newState);
}
if (thatSide.missionaries > 0 && thatSide.cannibals > 0)
{
final MCState newState =
new MCState(this,thisSide.both(1), thatSide.both(-1));
queueNewState(newStates, newState);
}
}
return newStates;
}
private void queueNewState(final ListnewStates, final MCState newState)
{
if (newState.isValid())
{
newStates.add(newState);
}
}
private boolean isValid()
{
return (thisSide.missionaries == 0 || thisSide.missionaries >= thisSide.cannibals)
&& (thatSide.missionaries == 0 || thatSide.missionaries >= thatSide.cannibals);
}
@Override
public String toString()
{
final String format = (boatSide == BoatSide.THIS) ? "%s * -> %s" : "%s -> * %s";
return String.format(format, thisSide, thatSide);
}
@Override
public boolean equals(final Object o)
{
if (! (o instanceof MCState)) return false;
final MCState other = (MCState) o;
return this.thisSide.equals(other.thisSide)
&& this.thatSide.equals(other.thatSide)
&& this.boatSide == other.boatSide;
}
@Override
public int hashCode()
{
return thisSide.hashCode() ^ thatSide.hashCode() ^ boatSide.hashCode();
}
}
That is a fair amount of code, and nicely tedious. The key points, though, are the implementation of the State interface; the State knows whether or not it is a goal, and it knows how to generate the next states, following immediate, single step actions.
After that big wall o' code, you are probably waiting for a punch line. Unfortunately, there isn't one. Just a driver class invoking the search twice with a couple of different queue parameters. The first option uses ArrayDeque, which implements a First-In, First-Out queue.
Queuefifo = new ArrayDeque ();
Searchsearch = new Search (fifo, new HashSet (), new MCState());
MCState end = search.findGoal();
The second option uses an anonymous subclass of ArrayDequeue where remove calls removeLast rather than removeFirst. As a result, it implements a Last-In, First-Out queue, or a stack.
Queuelifo = new ArrayDeque () {
@Override
public MCState remove()
{
return super.removeLast();
}
};
Searchsearch = new Search (lifo, new HashSet (), new MCState());
MCState end = search.findGoal();
These two options are my first demonstration of the flexibility of the state space search algorithm. Using a FIFO queue searches the state space breadth-first, visiting all of the states at a given distance from the initial state before any states at a greater distance. Using a LIFO queue searches the state space depth-first, visiting all of the states following a given state before visiting any other states. The difference in this case is modest; a FIFO queue visits 16 states while a LIFO queue visits 13 to find a solution. But that is just the tip of the iceberg.
Update: completely forgot about this. If you want to try it yourself, there is a related problem involving a farmer crossing a river. The farmer is carrying a bushel of corn, a duck, and a fox. (Yeah, I don't really get it either.) If the duck is left unattended with the corn, the corn gets eaten. If the fox is left unattended with the duck, the duck gets eaten. The boat will only carry the farmer and one of the other items. How can the farmer get to the other side of the river with the corn, duck, and fox intact? You can get the state space search code, such as it is, and you will need to write a State for the problem similar to MCState and a driver program.
For the continuing story of state space search, check out the next post, State space search: heuristics and State space search: A*.
You can get the code on github. I owe a considerable debt to Gerhard Wickler for his problem definition and illustration. He has a Java library of documented search code that you might want to check out as well.
Update 20 Nov 2012: Relevant.
